Delving into the fascinating world of geometry, we embark on a journey to uncover the intriguing properties of kites and trapezoids. These captivating shapes possess unique characteristics that define their form and function, offering a rich tapestry of mathematical insights.
From the graceful ascent of kites soaring through the sky to the structural integrity of trapezoids in architecture, these shapes play a significant role in our world. Join us as we explore the intricacies of their properties, unraveling the secrets that lie within their geometric contours.
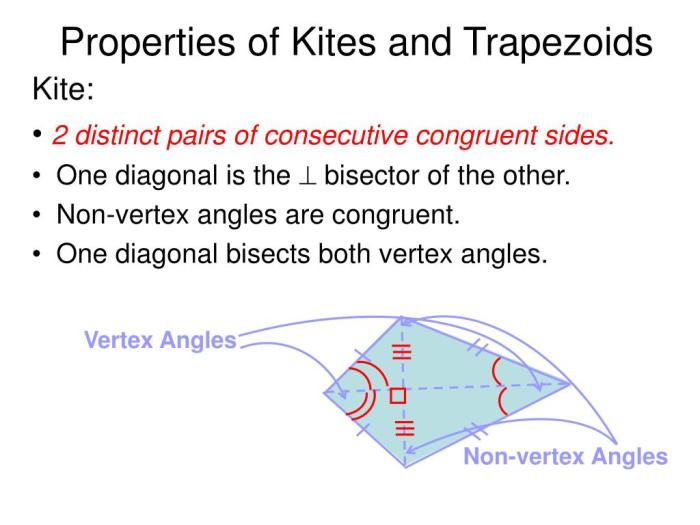
Kite Properties

Kites are versatile objects that have captured the fascination of people for centuries. They come in a wide variety of shapes and sizes, each with its unique flight characteristics.
The basic aerodynamics of a kite are relatively simple. When the kite is flown into the wind, the air flowing over the kite’s surface creates a pressure difference. The air pressure on the top of the kite is lower than the air pressure on the bottom, which creates lift.
The lift force opposes the weight of the kite, keeping it in the air.
The shape of the kite plays a significant role in its flight characteristics. Different shapes of kites produce different amounts of lift and drag, which affects how well the kite flies.
Types of Kites
| Type of Kite | Shape |
|---|---|
| Single-line kite | Flat, triangular shape |
| Dual-line kite | Flat, rectangular shape |
| Quad-line kite | Flat, diamond shape |
| Box kite | Three-dimensional, box shape |
| Delta kite | Triangular shape with a swept-back wing |
The factors that affect the flight characteristics of a kite include the wind speed, the wind direction, the weight of the kite, and the length of the kite string.
Trapezoid Properties
Trapezoids are quadrilaterals that have two parallel sides. They are often used in architecture and design because of their versatility and stability.
Properties of Trapezoids, Properties of kites and trapezoids
| Property | Description |
|---|---|
| Base angles | The two angles that are formed by the parallel sides |
| Leg lengths | The lengths of the two non-parallel sides |
| Area formula | A = (b1 + b2)
|
Trapezoids can be classified into three types: isosceles, scalene, and right trapezoids.
- Isosceles trapezoids have two equal non-parallel sides.
- Scalene trapezoids have no equal sides.
- Right trapezoids have one right angle.
Trapezoids are commonly found in everyday objects, such as tables, windows, and roofs.
Similarities and Differences between Kites and Trapezoids: Properties Of Kites And Trapezoids
Kites and trapezoids are both geometric shapes with four sides. However, there are also some key differences between the two shapes.
- Kites have two non-parallel sides, while trapezoids have only one pair of parallel sides.
- Kites are typically used for recreation, while trapezoids are often used in architecture and design.
Despite their differences, kites and trapezoids are both interesting and versatile shapes with a wide range of applications.
Applications of Kites and Trapezoids
Kites have been used for centuries for a variety of purposes, including recreation, sports, and scientific research.
- Kites are popular recreational activities for people of all ages.
- Kites are used in sports such as kiteboarding and kitesurfing.
- Kites are used in scientific research to study the atmosphere and to collect data.
Trapezoids are used in a wide variety of applications, including architecture, design, and engineering.
- Trapezoids are used in architecture to create roofs, windows, and other structural elements.
- Trapezoids are used in design to create logos, artwork, and other visual elements.
- Trapezoids are used in engineering to create bridges, buildings, and other structures.
Kites and trapezoids are both versatile shapes with a wide range of applications. Their unique properties make them useful for a variety of purposes, from recreation to scientific research.
FAQ Section
What is the key difference between a kite and a trapezoid?
While both kites and trapezoids have four sides, kites have two pairs of adjacent sides that are congruent, while trapezoids have only one pair of congruent sides.
How is the area of a trapezoid calculated?
The area of a trapezoid is calculated using the formula: Area = (1/2) x (base1 + base2) x height
What are some real-world applications of kites?
Kites have been used for centuries for various purposes, including recreation, sports, scientific research, and even military applications.

